История развития геометрии

Важность

Перед тем была представлена Бельтрами, Клейном и Пуанкаром в модели неевклидовой плоскости, геометрия Евклида стояла неоспоримую как математическая модель в пространстве . Более того, поскольку суть предмета в синтетической геометрии была главным проявлением рациональности, евклидова точка зрения представляла абсолютный авторитет.

Открытие неевклидовой геометрии имело волновой эффект, выходящий далеко за рамки математики и естественных наук. Отношение философа Иммануила Канта к человеческому знанию сыграло особую роль в геометрии. Это был его главный пример синтетического априорного знания; не выведенные из органов чувств и не выведенные с помощью логики — наши знания о космосе были истиной, с которой мы родились. К несчастью для Канта, его концепция этой неизменно истинной геометрии была евклидовой. На богословие также повлиял переход от абсолютной истины к относительной истине в том, как математика соотносится с окружающим миром, что явилось результатом этой смены парадигмы.

Неевклидова геометрия является примером научной революции в истории науки , когда математики и ученые изменили свой взгляд на свои предметы. Некоторые геометры называли Лобачевского « Коперником геометрии» из-за революционного характера его работ.

Существование неевклидовой геометрии во многом повлияло на интеллектуальную жизнь виклидской Англии и, в частности, было одним из ведущих факторов, вызвавших пересмотр преподавания геометрии, основанного на Элементах Евклида . В то время этот вопрос об учебной программе горячо обсуждался и даже стал предметом книги « Евклид и его современные соперники» , написанной Чарльзом Латвиджем Доджсоном (1832–1898), более известным как Льюис Кэрролл , автором « Алисы в стране чудес» .

«Начала» Евклида

Ватиканский манускрипт, т.1, 38v — 39r. Euclid I prop. 47 (теорема Пифагора)

Основное сочинение Евклида называется Начала. Книги с таким же названием, в которых последовательно излагались все основные факты геометрии и теоретической арифметики, составлялись ранее Гиппократом Хиосским, Леонтом и Февдием. Однако Начала Евклида вытеснили все эти сочинения из обихода и в течение более чем двух тысячелетий оставались базовым учебником геометрии. Создавая свой учебник, Евклид включил в него многое из того, что было создано его предшественниками, обработав этот материал и сведя его воедино.

Начала состоят из тринадцати книг. Первая и некоторые другие книги предваряются списком определений. Первой книге предпослан также список постулатов и аксиом. Как правило, постулаты задают базовые построения (напр., «требуется, чтобы через любые две точки можно было провести прямую»), а аксиомы — общие правила вывода при оперировании с величинами (напр., «если две величины равны третьей, они равны между собой»).

Евклид открывает врата Сада Математики. Иллюстрация из трактата Никколо Тартальи «Новая наука»

В I книге изучаются свойства треугольников и параллелограммов; эту книгу венчает знаменитая теорема Пифагора для прямоугольных треугольников. Книга II, восходящая к пифагорейцам, посвящена так называемой «геометрической алгебре». В III и IV книгах излагается геометрия окружностей, а также вписанных и описанных многоугольников; при работе над этими книгами Евклид мог воспользоваться сочинениями Гиппократа Хиосского. В V книге вводится общая теория пропорций, построенная Евдоксом Книдским, а в VI книге она прилагается к теории подобных фигур. VII—IX книги посвящены теории чисел и восходят к пифагорейцам; автором VIII книги, возможно, был Архит Тарентский. В этих книгах рассматриваются теоремы о пропорциях и геометрических прогрессиях, вводится метод для нахождения наибольшего общего делителя двух чисел (известный ныне как алгоритм Евклида), строятся чётные совершенные числа, доказывается бесконечность множества простых чисел. В X книге, представляющей собой самую объёмную и сложную часть Начал, строится классификация иррациональностей; возможно, что её автором является Теэтет Афинский. XI книга содержит основы стереометрии. В XII книге с помощью метода исчерпывания доказываются теоремы об отношениях площадей кругов, а также объёмов пирамид и конусов; автором этой книги по общему признанию является Евдокс Книдский. Наконец, XIII книга посвящена построению пяти правильных многогранников; считается, что часть построений была разработана Теэтетом Афинским.

В дошедших до нас рукописях к этим тринадцати книгам прибавлены ещё две. XIV книга принадлежит александрийцу Гипсиклу (ок. 200 г. до н. э.), а XV книга создана во время жизни Исидора Милетского, строителя храма св. Софии в Константинополе (начало VI в. н. э.).

Начала предоставляют общую основу для последующих геометрических трактатов Архимеда, Аполлония и других античных авторов; доказанные в них предложения считаются общеизвестными. Комментарии к Началам в античности составляли Герон, Порфирий, Папп, Прокл, Симпликий. Сохранился комментарий Прокла к I книге, а также комментарий Паппа к X книге (в арабском переводе). От античных авторов комментаторская традиция переходит к арабам, а потом и в Средневековую Европу.

В создании и развитии науки Нового времени Начала также сыграли важную идейную роль. Они оставались образцом математического трактата, строго и систематически излагающего основные положения той или иной математической науки.

Геометрия и компьютерная графика

Компьютерная анимация (CGI) преображает сложные природные формы (такие, как лицо) в комплект несложных форм. Так, сложный объект создаётся за счет комбинации несложных объектов и может изменяться в следствии трансформации их геометрии. В базе данной идеи — изучения математиков, например, французско-американского ученого Бенуа Мандельброта, который в 1974 г. продемонстрировал, что естественные формы подчиняются правилам фрактальной размерности (неэвклидова геометрия), а в рамках классической евклидовой геометрии смогут быть измерены только примерно.

Компьютерная графика на основе фракталов Мандельброта

О том как знание математики позволяет заработать на майнинге криптовалюты.

Tags: «Начала» Евклида геометрия история математики

Шаблоны для склеивания

Зачастую школьники задаются вопросом, что можно сделать из бумаги к урокам труда или на выставку. Работы ученика выделятся среди остальных, если это будут сложные трехмерные предметы, рельефные геометрические фигуры, платоновы тела, шаблоны кристаллов и минералов.

Если следовать инструкции, то ученик 5–6 класса сможет без помощи родителей сделать точный додекаэдр или тетраэдр.

Иногда в школе задают логические задания, как из квадрата сделать круг или шестиугольник. Для этого определить центр квадрата, согнув его по диагонали. Точка пересечения прямых — центр квадрата и будущего круга. Исходя из этого, можно начертить круг.

Фигурок из треугольников

Макетирование — увлекательное занятие. Оно помогает развить воображение и логическое мышление. Из бумаги делают не только фигуры, но и необычные скульптуры, статуэтки, шестиугольные–двенадцатиугольные предметы, наклонные объекты (например, Пизанскую башню), карандаши, линейки. На фото и картинках можно посмотреть, как выглядят оригинальные поделки из бумаги.

Школьники младших классов или дошколята делают бумажные объемные поделки. Например, предметы из овала — веер, цветы, гусеницы. Для них потребуются овалы и круги разного диаметра. Раскладки склеиваются между собой, получаются трехмерные игрушки.

Начинающие конструкторы задаются вопросами, как рисовать и чертить геометрические фигуры, как правильно склеить выкройки и как делают врезки. Проще всего распечатать готовый шаблон. Затем необходимо согнуть фигуру по пунктирным линиям.

Чтобы сгибы получились ровными, к пунктиру прикладывают линейку, по ее форме делают точные загибы. Такой способ особенно помогает, когда речь идет о фигурках из картона или ребенок делает самые сложные макеты. Например, икосаэдр, додекаэдр, тетраэдр.

На последнем этапе необходимо скрепить элементы объекта, места для склейки обозначены на развернутом виде фигуры. Детали из картона приклеивают при помощи ПВА, а бумажные — карандашным клеем.

Основные ошибки при работе с моделями:

Ребенок делает неправильные сгибы — например, изгиб отклоняется в сторону от пунктира на несколько градусов. В результате модель получится неточной.

Неточности во время вырезания шаблонов. Если малыш отрезал одну из границ для склеивания, то фигурка будет разворачиваться. Здесь на помощь придет взрослый.

Оригами – бумажные фигурки, которые относятся к японскому искусству и существуют в нём уже не одно столетие. Монахи ещё в древние времена, использовали фигурки из бумаги для декорации храмов и его залов, а также для применения их в религиозных целях (осуществление обрядов).

Сделать оригами из бумаги своими руками в состоянии каждый малоопытный мастер, но главным критерием есть имение усидчивости и точности движений. Сегодня вы поймёте, что не нужно быть асом, чтобы красиво сделать эти изделия.

Практическая сторона геометрии

Название «геометрия» переводится с греческого, как «гео» — земля и «метрео» — мерить. Изначально геометрию использовали для разметки земли и других работ с землей. Но, оказалось, что сфера ее влияния безгранична.

Чтобы понять, зачем нам нужны знания по геометрии, просто оглянитесь вокруг: геометрия окружает нас в предметах разных форм. Взять хотя бы круг: его используют в искусстве, строительстве, технике. То же самое и с другими фигурами: чтобы сконструировать автомобиль или айфон, сшить одежду или построить дом — не обойтись без геометрии.

А еще геометрия помогает научиться рассуждать логически, искать связи и противоречия — полезный навык в диджитал-мире, когда информация окружает нас повсюду.

Вот, в каких профессиях пригодится геометрия: архитектор, айтишник, дизайнер, инженер, конструктор, строитель, smm-менеджер, декоратор, летчик, водитель, художник, проектировщик, астроном, спортсмен, музыкант и другие.

Почему изучать геометрию просто: мы видим объемный мир каждый день и регулярно прикасаемся к предметам, строим планы, размышляем и считаем в уме. В геометрии все знания подкреплены научными теориями — это помогает взаимодействовать с пространством по-другому, более осознанно.

Почему изучать геометрию сложно: некоторые правила придется учить наизусть.

Чтобы понять геометрию, двигайтесь от простого к сложному. Многие теоремы могут показаться очевидными. Но эта видимость может быть верной только для одного рисунка. Невозможно нарисовать все ситуации, ведь их их бесконечное множество

Именно поэтому важно доказать истину, чтобы никогда не сомневаться в ней

Комбинации простейших объектов

Поговорим про комбинации простейших объектов. Например, две прямые, которые мы уже разглядели — либо пересекаются на плоскости, либо нет (тогда они параллельны).
 

Когда прямые пересекаются, можно ввести понятие отношения между двумя прямыми. Аналогично мы поступали с числами: ввели натуральные числа — количество предметов в множестве. А после этого изучали отношения между этими числами: дроби, возведение в степень.

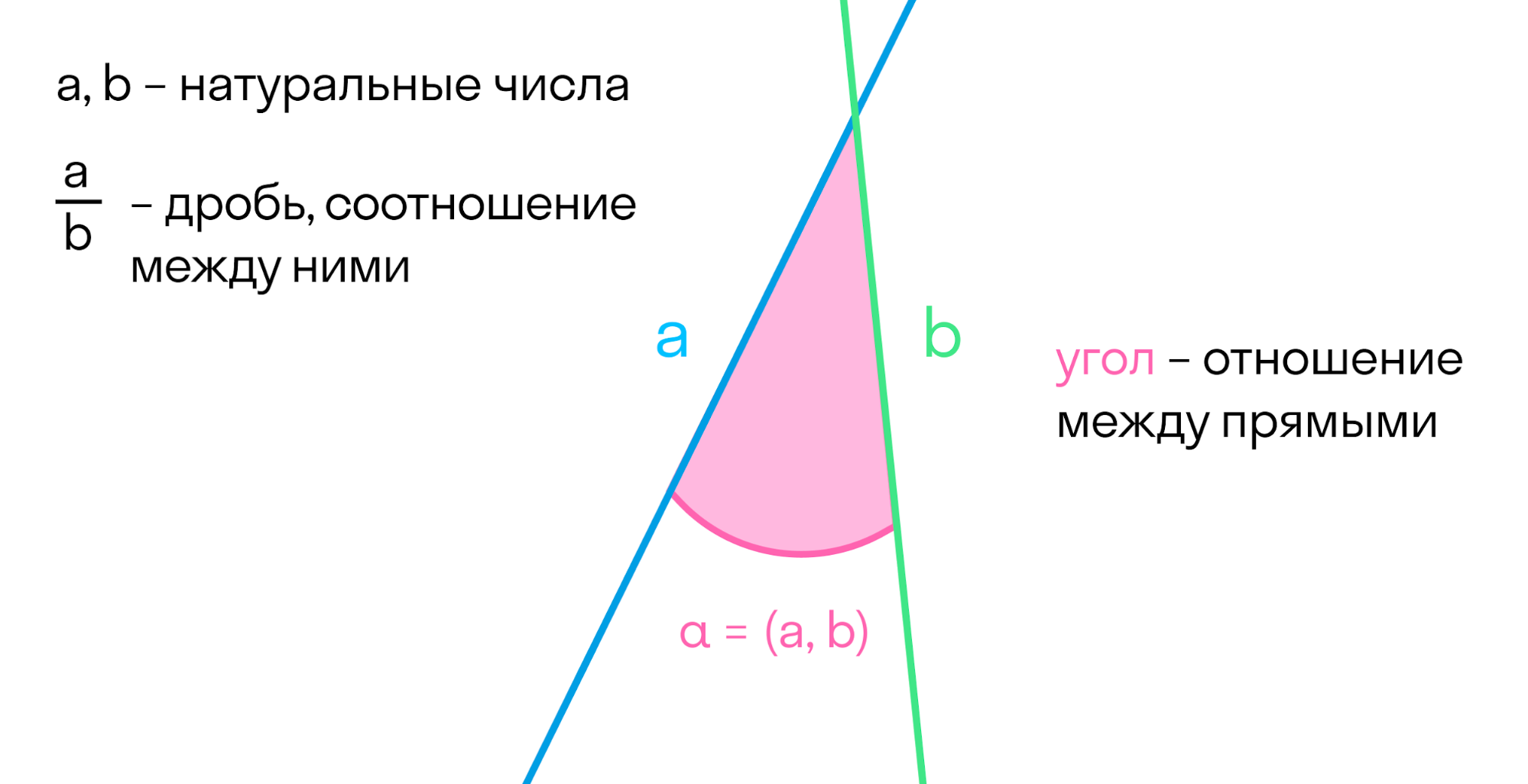
Точно так же мы изучали множества, а после — отношения между множествами, функции.

Две прямые образуют углы. По сути, угол — это отношение между прямыми. Если один из них нулевой, то прямые параллельны. Если нет — прямые пересекаются.
 

Максимальный угол – это полный оборот, он составляет 360 градусов.

Угол — это часть плоскости, ограниченная двумя лучами, которые выходят из одной точки. Углы измеряются в градусах. Углов бесконечно много, так как от 0° до 360° угол может принимать бесконечное множество значений.

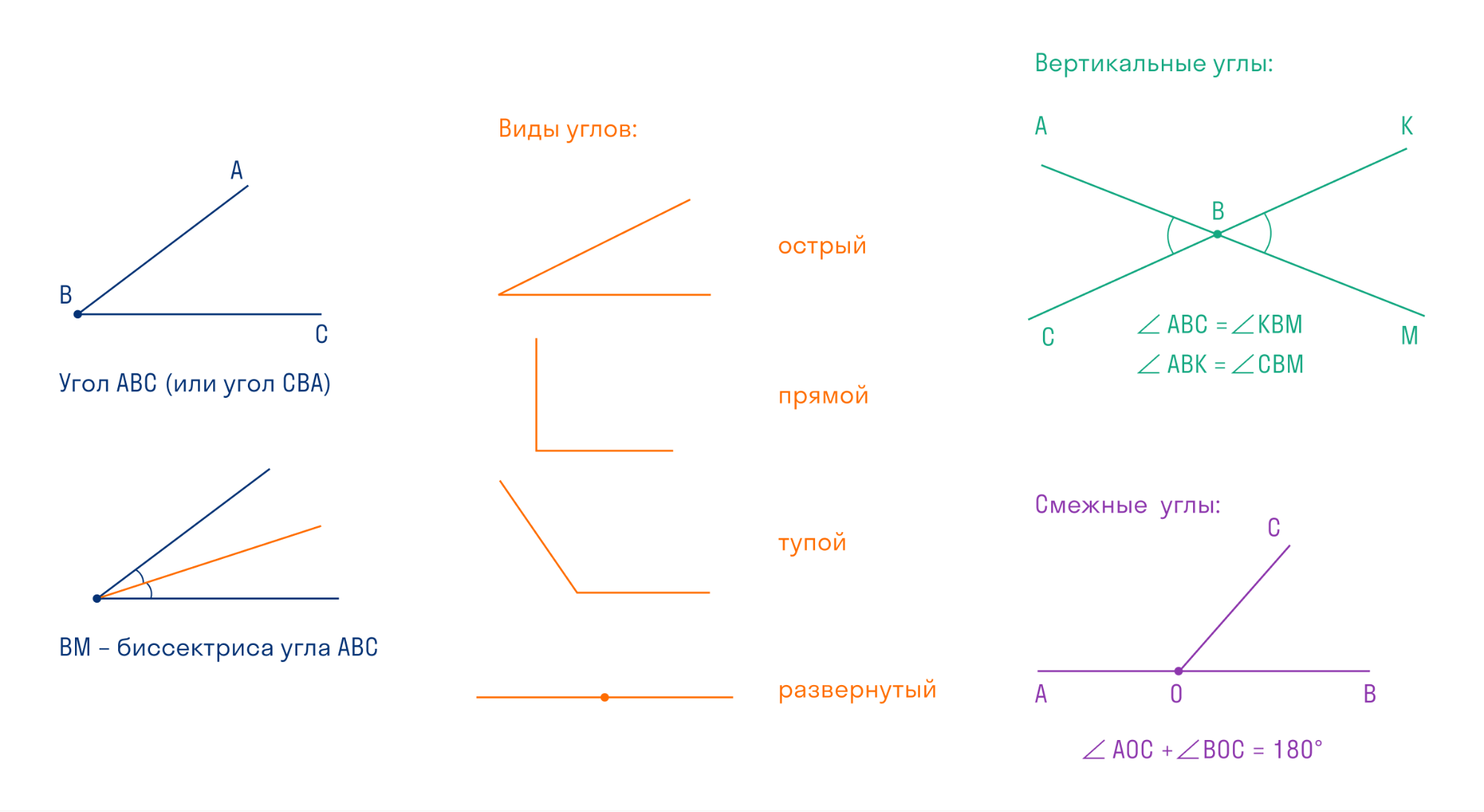
Есть разные виды углов, выделим самые часто встречающиеся:

• Если градусная мера угла меньше 90° — угол острый.
• Если градусная мера угла равна 90° — угол прямой.
• Если градусная мера угла больше 90°, но меньше 180° — угол тупой.
• Если градусная мера угла равна 180° — угол развернутый.

Точка называется вершиной угла, а лучи — сторонами угла.

Два угла называются вертикальными, если их стороны являются дополнительными лучами. Свойство вертикальных углов звучит так: вертикальные углы равны.

Два угла называются смежными, если одна сторона у них общая, а две другие являются дополнительными лучами. Свойство смежных углов: сумма смежных углов равна 180°.

Биссектриса угла — это луч с началом в вершине угла, который делит угол на две равные части.

А теперь посмотрим на взаимное расположение трех прямых.

Первый случай: все три прямые параллельны.

Второй случай: две прямые параллельны, а третья их пересекает.

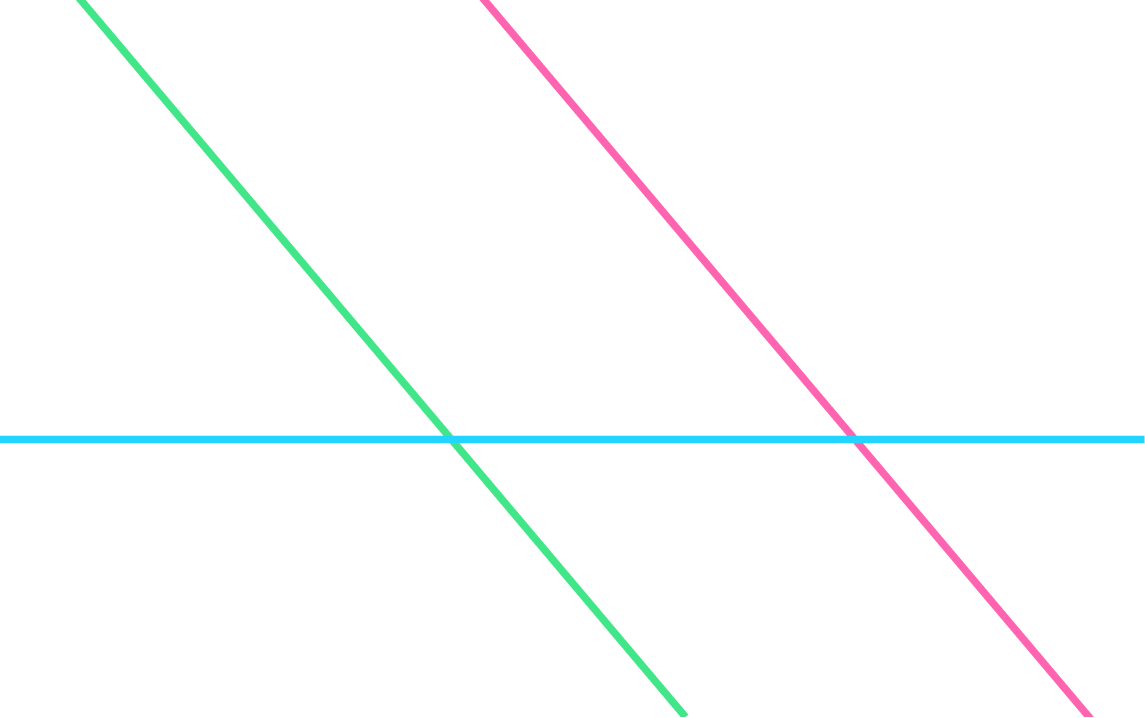
Третий случай: если провести три прямые на плоскости случайным образом, велика вероятность образования треугольника. Поэтому этой фигуре мы уделяем так много времени в школе на уроках геометрии.

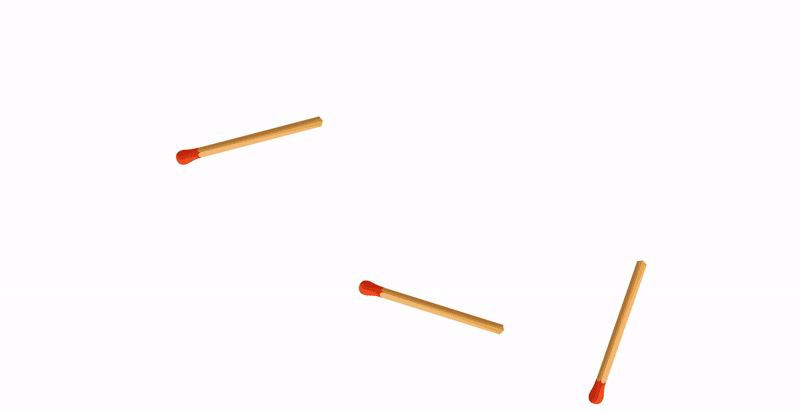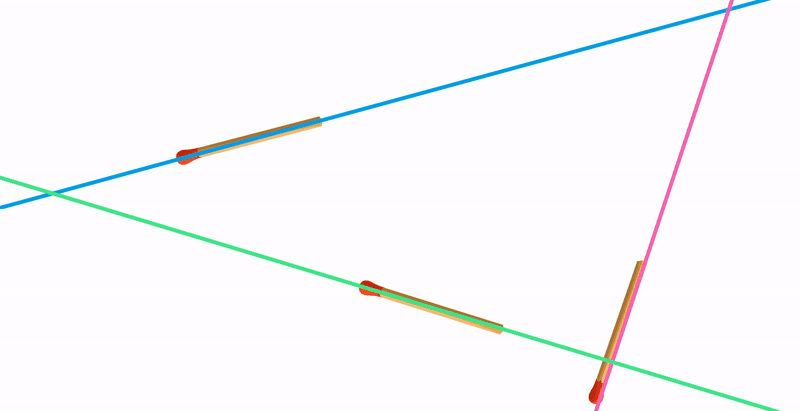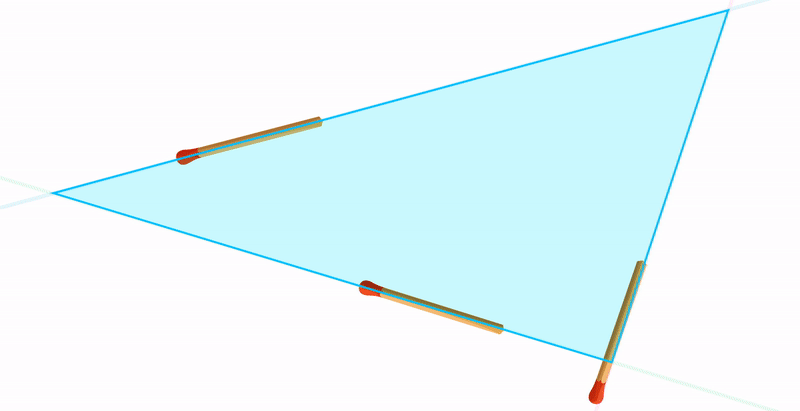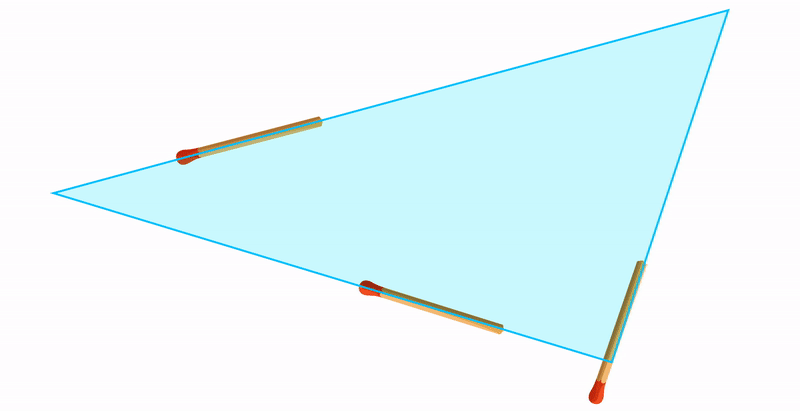
Эпонимы

Следующие математические структуры названы в честь Евклида:

• Евклидово расстояние , длина прямой связи между двумя точками на плоскости или в пространстве.
• Евклидов алгоритм , метод вычисления наибольшего общего делителя двух натуральных чисел
• Евклидова геометрия , начертательная геометрия плоскости или пространства
• Евклидово твердое тело , упорядоченное твердое тело, в котором каждый неотрицательный элемент имеет квадратный корень
• Евклидова норма , длина вектора на плоскости или в пространстве
• Евклидово пространство , пространство интуиции, реальное аффинное пространство со стандартным скалярным произведением
• Евклидово отношение , отношение, к которому применимо следующее: если два элемента связаны каждый с третьим, то они также связаны друг с другом.
• Евклидово кольцо , кольцо, в котором возможно деление на остаток
• Евклидовы инструменты , допустимые действия при построении с циркулем и линейкой

Кроме того, в честь Евклида названы следующие математические теоремы и доказательства:

• Евклидово доказательство иррациональности корня из 2 , первое доказательство противоречия в истории математики
• Теорема Евклида о высоте : в прямоугольном треугольнике квадрат над высотой равен по площади прямоугольнику из сечений гипотенузы.
• Теорема Евклида о катетерах : в прямоугольном треугольнике квадраты катета равны произведению гипотенузы и соответствующего сечения гипотенузы.
• Лемма Евклида : если простое число делит произведение двух чисел, то также хотя бы один из двух множителей
• Теорема Евклида : простых чисел бесконечно много

Также назван в честь Евклида:

• Евклид (лунный кратер) , кратер на передней части Луны
• (4354) Евклид , астероид главного пояса

Пифагорова тройка

Пифагорова тройка из трёх натуральных чисел (x,y,z)удовлетворяет соотношению Пифагора: x2+y2=z2. При этом числа, образующие пифагорову тройку, называются пифагоровыми числами. Треугольник, длины сторон которого равны пифагоровым числам, является прямоугольным. Простейший из них — египетский треугольник со сторонами 3,4,5: 32+42=52.

Некоторые пифагоровы тройки : (3, 4, 5), (6, 8, 10), (5, 12, 13), (9, 12, 15), (8, 15, 17), (12, 16, 20), (15, 20, 25), (7, 24, 25), (10, 24, 26), (20, 21, 29), (18, 24, 30), (16, 30, 34),(21, 28, 35), (12, 35, 37), (15, 36, 39), (24, 32, 40), (9, 40, 41), (27, 36, 45), (14, 48, 50), (30, 40, 50), …Пифагоровы тройки известны очень давно. В архитектуре древнемесопотамских надгробий встречается равнобедренный треугольник, составленный из двух прямоугольных со сторонами 9, 12 и 15 локтей. Пирамиды фараона Снофру (XXVII век до н. э.) построены с использованием треугольников со сторонами 20, 21 и 29, а также 18, 24 и 30 десятков египетских локтей.

Рекомендации

• А’Кампо, Норберт и Пападопулос, Атанас , (2012) Заметки о гиперболической геометрии , в: Страсбургский мастер-класс по геометрии, стр. 1–182, Лекции IRMA по математике и теоретической физике, Vol. 18, Цюрих: Европейское математическое общество (EMS), 461 страница, ISBN  978-3-03719-105-7 , DOI: 10.4171 / 105 .
• Андерсон, Джеймс В. Гиперболическая геометрия , второе издание, Springer, 2005 г.
• Бельтрами, Eugenio Teoria fondamentale degli spazî di curvatura costante , Аннали. ди Мат., серия II 2 (1868), 232–255
• Блюменталь, Леонард М. (1980), Современный взгляд на геометрию , Нью-Йорк: Довер, ISBN 0-486-63962-2
• Кэрролл, Льюис Евклид и его современные соперники , Нью-Йорк: Барнс и Ноубл, 2009 (перепечатка) ISBN  978-1-4351-2348-9
• HSM Coxeter (1942) Неевклидова геометрия , University of Toronto Press , переиздано в 1998 году Математической ассоциацией Америки , ISBN  0-88385-522-4 .
• Фабер, Ричард Л. (1983), Основы евклидовой и неевклидовой геометрии , Нью-Йорк: Марсель Деккер, ISBN 0-8247-1748-1
• Джереми Грей (1989) Идеи пространства: евклидово, неевклидово и релятивистское , 2-е издание, Clarendon Press .
• Гринберг, Марвин Джей Евклидова и неевклидова геометрия: развитие и история , 4-е изд., Нью-Йорк: WH Freeman, 2007. ISBN  0-7167-9948-0
• Моррис Клайн (1972) Математическая мысль от древних до наших дней, глава 36, Неевклидова геометрия, стр. 861–81, Oxford University Press .
• Бернард Х. Лавенда , (2012) «Новый взгляд на теорию относительности: одиссея в неевклидовой геометрии», World Scientific , стр. 696, ISBN   .
• Николай Лобачевский (2010) Пангеометрия , переводчик и редактор: А. Пападопулос, Серия «Наследие европейской математики», Vol. 4, Европейское математическое общество .
• Мэннинг, Генри Паркер (1963), Введение в неевклидову геометрию , Нью-Йорк: Дувр
• Мешковский, Герберт (1964), Неевклидова геометрия , Нью-Йорк: Academic Press
• Милнор, Джон В. (1982) , Bull. Амер. Математика. Soc. (NS) Том 6, номер 1, стр. 9–24.
• Ричардс, Джоан Л. (1988), Математические видения: стремление к геометрии в викторианской Англии , Бостон: Academic Press, ISBN 0-12-587445-6
• Смарт, Джеймс Р. (1997), Современная геометрия (5-е изд.) , Pacific Grove: Brooks / Cole, ISBN 0-534-35188-3
• Стюарт, Ян (2001) Флаттерленд , Нью-Йорк: ISBN  издательства Perseus 0-7382-0675-X ( мягкая обложка )
• Джон Стиллвелл (1996) Источники гиперболической геометрии , ISBN Американского математического общества 0-8218-0529-0 . 
• Трюдо, Ричард Дж. (1987), , Бостон: Birkhauser, ISBN 0-8176-3311-1
• A. Papadopoulos et Guillaume Théret (2014) La théorie des parallèles de Johann Heinrich Lambert , (Критическое издание мемуаров Ламбера с французским переводом, с историческими и математическими примечаниями и комментариями — изд. Blanchard, Coll. Sciences dans l’Histoire, Paris ISBN  978-2-85367-266-5

Неевклидова геометрия

В геометрии Евклида имеется аксиома о параллельных, утверждающая: через точку, не лежащую на данной прямой, можно провести не более чем одну прямую, параллельную данной. Многие геометры пытались доказать эту аксиому, исходя из других основных посылок геометрии Евклида, но безуспешно. Лобачевский пришёл к мысли, что такое доказательство невозможно. Утверждение, противоположное аксиоме Евклида, гласит: через точку, не лежащую на данной прямой, можно провести не одну, а по крайней мере две параллельные ей прямые. Это и есть аксиома Лобачевского. По мысли Лобачевского, присоединение этого положения к другим основным положениям геометрии приводит к логически безупречным выводам. Система этих выводов и образует новую, неевклидову геометрию.
Заслуга Лобачевского состоит в том, что он не только высказал эту идею, но действительно построил и всесторонне развил новую геометрию, логически столь же совершенную и богатую выводами, как евклидова, несмотря на её несоответствие обычным наглядным представлениям.
Геометрия превратилась в разветвлённую и быстро развивающуюся в разных направлениях совокупность математических теорий, изучающих разные пространства (евклидово, Лобачевского, проективное, римановы и т. д.) и фигуры в этих пространствах.

Краткая биография

Биография Евклида до конца не изучена, к примеру, до сих пор неизвестен год рождения. Известно, что он появился на свет в небольшом районе Афин и был платоновским учеником.

Подъем его научной работы пришелся на правление Птолемея Первого. Некоторые сведения о его жизни можно проследить по арабским рукописям и архимедовым письмам к друзьям. Так, по ним можно определить, что Евклид был сыном греческого ученого и жил около Тира в Сирии.

С малых лет получал знания о мире от своего отца, он же привил сыну любовь к естественным наукам, а затем Евклид поступил в школу Платона, где и обучился математическим основам.

Повзрослев, его пригласили в храм Мусейон (по другим данным он был одним из его основателей), в котором собирались видные ученые с поэтами. Тут были классы для занятий. Также храм был заполнен садами с башнями астрономии, помещениями для одиноких размышлений и большой библиотекой.

В Мусейоне он смог открыть школу с лучшими математиками и монументальный труд в области математики, в котором заложил планиметрические основы со стереометрией, теорией чисел, законами алгебры, методами нахождения площадей с объемами и др.

Фрагмент папируса с текстом «Начал» Евклида

Монументальный труд — публикация «Начала». Это серия из 13 книг, представляющая собой обработанные публикации древнегреческих математиков с пятого по четвертый век до нашей эры.

Кроме «Начал», было создано еще одно сочинение — «Данные», в котором были опубликованы основы по геометрическому анализу. Кроме того, александрийский ученый создал учебник, с помощью которого в то время и сейчас изучают астрономию, перспективу, отражение в зеркале, музыкальные интервалы и решают тригонометрические задачи.

Все оставшиеся годы жизни посвятил изучению естественных наук и математических законов, отчего его называют отцом геометрии. О других аспектах его жизни неизвестно до сих пор. Умер в Александрии.

Это интересно: 231,ДУХОВНАЯ КУЛЬТУРА — разбираемся внимательно

Платон

Платон, живший в 428348 годах до нашей эры, считается, и, должно быть, справедливо я не специалист одним из величайших философов Греции.

Геометрия ко времени Платона уже была очень развита. Было решено много весьма и весьма сложных задач, доказаны сложнейшие теоремы. Но ясной позиции во взглядах на общую схему построения науки ещё не было. Развитие геометрии, как нередко бывает в науке, стимулировалось задачами, решения которых никак не удавалось отыскать. Требовалось при помощи циркуля и линейки, не привлекая никаких других геометрических инструментов:

• разделить данный угол на три равных части (трисекция угла);
• построить квадрат с площадью, равной площади данного круга (квадратура круга);
• построить куб с объёмом, в два раза большим объёма данного куба (делосская задача).

Только в конце прошлого века было доказано, что в такой постановке ни одна из этих задач не может быть решена, хотя, если использовать другие геометрические инструменты или (что то же) использовать при построении геометрические места точек, отличные от прямой либо дуги окружности, то все три задачи легко решаются.

Однако принятые у греков правила игры не позволяли пользоваться при решении задач ничем, кроме циркуля и линейки. Платон даже обосновал это ссылкой на авторитет богов.

Так что ни одна из проблем решена не была, но по ходу дела геометрия была основательно разработана.

Я с великим сожалением опускаю все анекдоты, связанные с этими задачами. Историй много, и все они прелестны, но нельзя слишком отвлекаться. Вспомню лишь одно из преданий, связанное именно с Платоном и показывающее его с лучшей стороны.

Однажды, рассказывает Эратосфен, на острове Делосе вспыхнула эпидемия чумы. Жители острова, естественно, обратились к Дельфийскому оракулу, который повелел удвоить объём золотого кубического жертвенника Аполлону, не изменяя его формы. За советом обратились к Платону. Платон задачи не решил, но зато истолковал оракула в том смысле, что боги гневаются на греков за нескончаемые междоусобные войны и желают, чтобы они, греки, вместо кровавых побоищ занимались бы науками и особенно геометрией. Тогда чума исчезнет.

Платон очень много сделал для развития математики и весьма ценил её. На входе в его академию был даже высечен весьма категорический лозунг: «Да не войдёт сюда тот, кто не знает геометрии». Дело в том, что Платон полагал: «Изучение геометрии приближает к бессмертным богам» и воспитывал в этом духе своих учеников, приплетая математику к месту и не к месту.

По-видимому, Платон первый чётко потребовал: математика вообще и геометрия в частности должны быть построены дедуктивным образом. Иначе говоря, все утверждения (теоремы) должны строго логически выводиться из небольшого числа основных положений аксиом. Такая постановка крупнейший шаг вперёд.

Некоторые из учеников Платона выросли в блестящих геометров. Но надо сказать, что и по своим взглядам, и по методам организации школы, и по любви к саморекламе Платон очень напоминает Пифагора.

На мой взгляд, как философ и как человек, Платон довольно несимпатичен. Во всяком случае, созданная им теория идеального государства, образцом которого послужила реальная и вполне фашистская страна Спарта восторга, мягко говоря, не вызывает. Основные положения его утопии в общем удовлетворяют требованиям нацистов. Всю свою жизнь он яростно боролся против демократии в политической жизни и против материализма в духовной. Философов-материалистов Платон не только абстрактно поносил в своих философских сочинениях, но, демонстрируя неплохую практическую хватку, нередко дискутировал, как сказали бы теперь, «в жанре политического доноса».

Приведу пример. Был в те времена в Греции замечательный философ, один из первых материалистов Анаксагор. (Мы почти ничего не знаем о его геометрических работах; известно, однако, что в темнице, где ему пришлось сидеть за свои взгляды, он исследовал проблему квадратуры круга.)

И вот Платон в одном из сочинений в диалоге жителя Афин (рупор самого Платона) и спартанца так расправляется с Анаксагором.

Афинянин: «Когда мы, стремясь получить доказательства существования богов, ссылаемся на Солнце, Луну, Звёзды и Землю как на божественные существа, то ученики этих новых мудрецов возражают нам, что всё это ведь только земля и камни, и они (т.е. камни) совершенно не в состоянии заботиться о людских делах».

Спартанец молниеносно чует ересь и возмущённо восклицает: «Какой же вред для семьи и государства проистекает от таких настроений у молодёжи!».

Так дискутировал Платон.

Базовые геометрические объекты

Базовые геометрические фигуры — это точки, отрезки, лучи, прямые, плоскости.

Точка — это идеальный математический объект, у которого нет длины и ширины.

Отрезок — это часть прямой, у которого есть начало и конец.

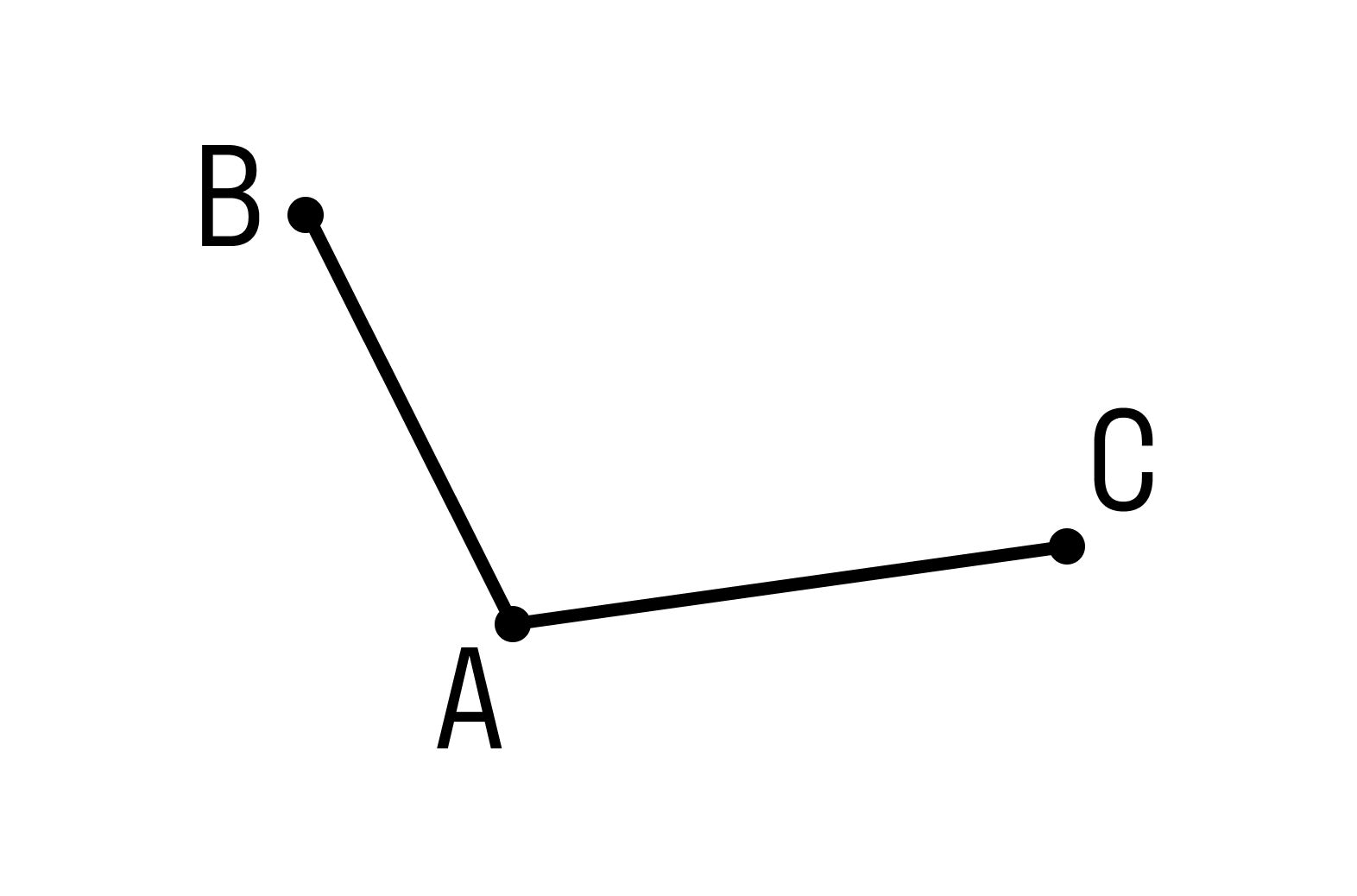
Смежные отрезки — это отрезки, которые не лежат на одной прямой и имеют один общий конец. На рисунке изобразили смежные отрезки АВ и АС, где точка А — общий конец.

Прямая — это «не кривая». Более точное определение вряд ли можно сформулировать.

Когда мы рисуем прямую на листе бумаги, мы изображаем только ее часть, потому что прямая не имеет начала и конца.

Обозначать прямые принято малыми латинскими буквами (a, b,c), но можно и большими латинскими буквами (АВ, CD, MN). Точки всегда обозначают большими латинскими буквами (А, В, С).

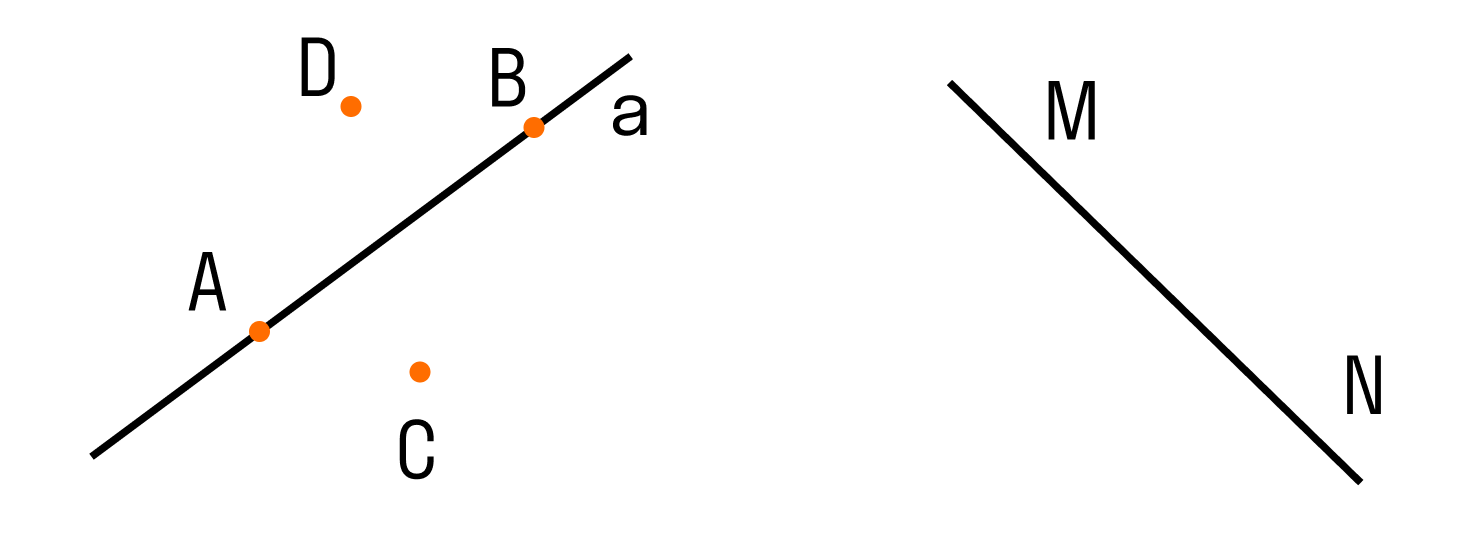
Два варианта расположения точек относительно прямой:

1. Точки лежат на данной прямой. Или еще говорят, что прямая проходит через эти точки — на рисунке выше такими точками являются А и В. При решении задач для краткости используют запись A ∈ a (читается так: точка А принадлежит прямой a или точка А лежит на прямой a), аналогично будет и для точки В (B ∈ b).
2. Точки не лежат на данной прямой. Говорят так: прямая не проходит через эти точки — на рисунке такими точками являются С и D. При решении задач для краткости используют запись C ∉ a (читается так: точка С не принадлежит прямой a или точка С не лежит на прямой a), аналогично будет и для точки D (D ∉ a).

Важно знать

Через любые две точки можно провести прямую и притом только одну.

Если рассмотреть две прямые, то возможны два варианта их расположения:

1. Прямые пересекаются, то есть имеют одну общую точку.
   Для записи пересекающихся прямых используют специальный знак — ∩ , то есть a ∩ b (читают: прямая a пересекает прямую b).
2. Прямые не пересекаются, то есть не имеют общих точек.
   Для записи не пересекающихся прямых используют специальный знак — ,
   то есть m n (читают: прямая m не пересекает прямую n).

Луч — это часть прямой, ограниченная с одной стороны. Луч имеет начало, но не имеет конца.

На рисунке точка О разбивает прямую АВ на две части:

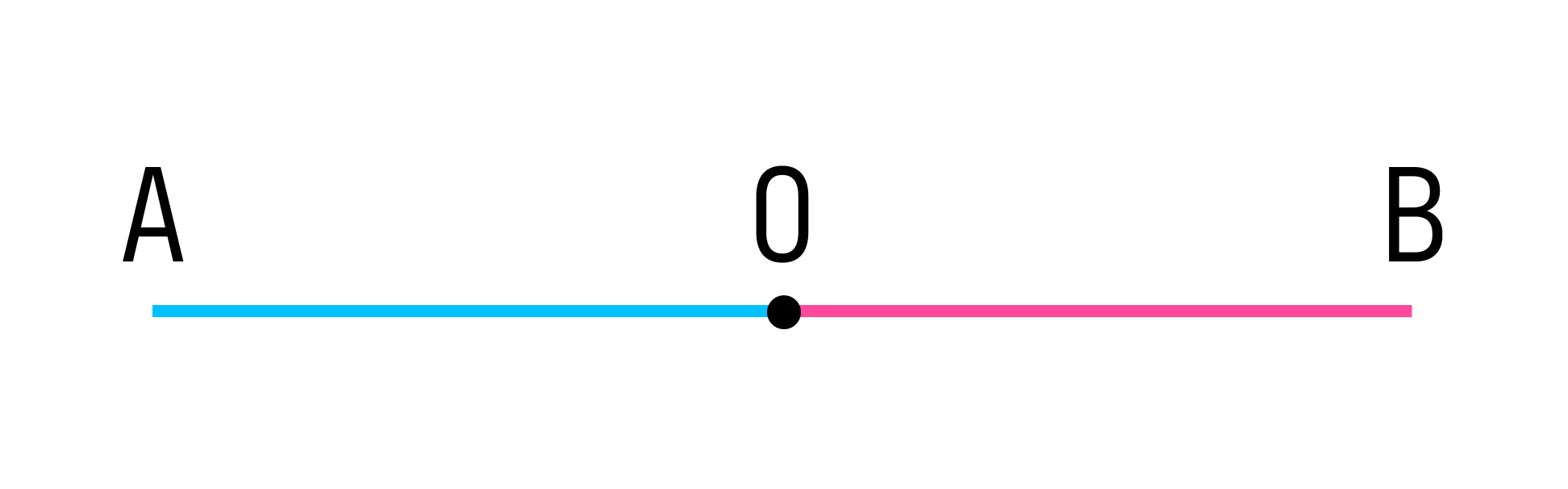
Каждая из этих частей называется лучом, а точка О является началом одного и другого луча.

Назовем получившиеся лучи:

• Луч ОА, точка О — начало луча ОА; конца у луча ОА нет.
• Луч ОВ, точка О — начало луча ОВ; конца у луча ОВ нет.

Лучи ОА и ОВ принадлежат одной прямой АВ. Лучи ОА и ОВ имеют общее начало (точка О). Лучи ОА и ОВ противоположно направлены. При таких условиях лучи ОА и ОВ называются дополнительными.

Плоскость — это бесконечная поверхность, к которой принадлежат все прямые, которые проходят через какие-либо две точки плоскости

История развития геометрии

Самые первые понятия в геометрии люди приобрели еще в глубокой древности. Возникала необходимость определять площади участков земли, объемы различных сосудов и помещений и другие практические потребности. Свое начало история развития геометрии, как науки, берет в Древнем Египте около 4 тысяч лет назад. Затем знания египтян позаимствовали древние греки, которые применяли их преимущественно для того, чтобы измерять площади земельных участков.  Именно с Древней Греции берет свое начало история возникновения геометрии, как науки. Древнегреческое слово «геометрия» переводится, как «землемерие».

Греческие ученые  на основе открытия множества геометрических свойств смогли создать стройную систему знаний по геометрии. В основу геометрической науки были положены простейшие геометрические свойства, взятые из опыта. Остальные положения науки выводились из простейших геометрических свойств с помощью рассуждений. Вся эта система была опубликована в завершенном виде в «Началах» Евклида около 300 года до нашей эры, где он изложил не только теоретическую геометрию, но и основы теоретической арифметики. С этого источника также начинается и история развития математики.

Однако в труде Евклида ничего не сказано ни об измерении объема, ни о поверхности шара, ни об отношении длины круга к его диаметру (хотя присутствует теорема о площади круга). История развития геометрии получила продолжение в середине III века до нашей эры благодаря великому Архимеду, который смог вычислит число Пи, а также смог определить способы вычисления поверхности шара. Архимед для решения упомянутых задач применил методы, которые в дальнейшем легли в основу методов высшей математики. С их помощью он уже мог решать трудные практические задачи геометрии и механики, которые были важны для мореплавания и для строительного дела. В частности, он нашел способы определять центры тяжести и объемы многих физических тел и смог изучить вопросы равновесия тел различной формы при погружении в жидкость.

Древнегреческие ученые провели исследования свойств различных геометрических линий, важных для теории науки и практических применений. Аполлоний во II веке до нашей эры сделал много важных открытии по теории конических сечений, которые оставались непревзойденными на протяжении следующих восемнадцати веков. Апполоний применил метод координат для изучения конических сечений. Этот метод в дальнейшем смогли развить только в XVII веке ученые Ферма и Декарт. Но они применяли этот метод только для изучения плоских линий. И только в 1748 году русский академик Эйлер смог применить этот метод для изучения кривых поверхностей.

Система, разработанная Евклидом, считалась непреложной более двух тысяч лет. Однако в дальнейшем история развития геометрии получила неожиданный поворот, когда в 1826 году гениальный русский математик Н.И. Лобачевский смог создать совершенно новую геометрическую систему. Фактически основные положения его системы отличаются от положений геометрии Евклида только в одном пункте, но именно из этого пункта вытекают основные особенности системы Лобачевского. Это положение о том, что сумма углов треугольника в геометрии Лобачевского всегда меньше 180 градусов. На первый взгляд может показаться, что это утверждение неверно, однако при маленьких размерах треугольников современные средства измерения не дают правильно измерить сумму его углов.

Дальнейшая история развития геометрии доказала правильность гениальных идей Лобачевского и показала, что система Евклида просто неспособна решить многие вопросы астрономии и физики, где математики имеют дело с фигурами практически бесконечных размеров. Именно с трудами Лобачевского уже связано дальнейшее развитие геометрии, а с ней и высшей математики и астрономии.

Планарные алгебры

В аналитической геометрии плоскость описывается декартовыми координатами  : С = {( х, у ): х , у ∈ ℝ}. Эти точки иногда идентифицированы с комплексными числами г = х + у е , где ε 2 ∈ {-1, 0, 1}.

Евклидова плоскость соответствует случаю ε 2 = −1, поскольку модуль z определяется выражением

zz*знак равно(Икс+уϵ)(Икс-уϵ)знак равноИкс2+у2{\ displaystyle zz ^ {\ ast} = (x + y \ epsilon) (xy \ epsilon) = x ^ {2} + y ^ {2}}

и эта величина является квадратом евклидова расстояния между z и началом координат. Например, { z | zz * = 1} — единичный круг .

Для плоской алгебры неевклидова геометрия возникает в других случаях. Когда ε 2 = +1 , тогда z является комплексным числом с разбиением и обычно j заменяет эпсилон. потом

zz*знак равно(Икс+уj)(Икс-уj)знак равноИкс2-у2{\ displaystyle zz ^ {\ ast} = (x + y \ mathbf {j}) (xy \ mathbf {j}) = x ^ {2} -y ^ {2} \!}

и { z | zz * = 1} — единичная гипербола .

Когда ε 2 = 0 , то z — двойственное число .

Такой подход к неевклидовой геометрии объясняет неевклидовы углы: параметры наклона в плоскости двойных чисел и гиперболический угол в плоскости расщепленного комплекса соответствуют углу в евклидовой геометрии. В самом деле, каждое из них возникает в комплексного числа z .

XX — го века

В XX — м  веке, традиционное деление математики в арифметике, алгебре, анализу, геометрии и взорвался, так что само определение того , что можно было бы назвать «геометрия работы» в части предмета для обсуждения.

Сегодня, когда используется слово «геометрия», рекомендуется различать, разрешено ли его использование во множественном числе.

Геометрия в том смысле, в котором это слово все еще присутствует в обычном языке, называется евклидовой геометрией, если мы хотим использовать математический язык, который хоть немного поддерживается. Эта часть математики считается по существу завершенной с точки зрения ее общей теории. В этом смысле, вопросы геометрии возможно падение прикладной математики и не также не глубокие исследований , проведенных в XX — го  века. Однако мы должны исключить вопросы, касающиеся основ аксиоматики евклидовой геометрии.

С другой стороны, согласно выводам программы Клейна, слово «геометрия» также широко используется во множественном числе в современной математике. В этом смысле он на самом деле не охватывает конкретную дисциплину, но, с другой стороны, пронизывает очень большую часть всех современных математических теорий.

Аксиоматика геометрии

После открытия особого характера геометрии Евклида переформулировка аксиом геометрии стала предметом целого ряда замечательных работ. Можно, в частности, процитировать работы Д. Гильберта по основам геометрии.

После Гильберта вопрос об аксиомах, которые необходимо сохранить для основания геометрии, был поднят, в частности, Биркгофом с эргодической теорией как водяным знаком и Тарским ( банаховы пространства конечной размерности ).

Множество методов аксиоматизации геометрии Евклида и неопределенность их полной идентичности ( например, парадокс Банаха-Тарского ) — одна из самых захватывающих загадок современной математики.